题目信息
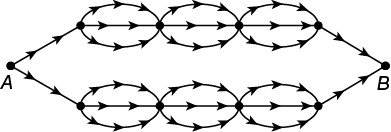
The map above shows the trails through a wilderness area. If travel is in the direction of the arrows, how many routes along the marked trails are possible from point A to point B ?
A:11
B:18
C:54
D:108
E:432
参考答案及共享解析

共享解析来源为网络权威资源、GMAT高分考生等; 如有疑问,欢迎在评论区提问与讨论
本题耗时:
已选答案:
正确答案:
C:54
Arithmetic Elementary combinatorics
It is clear that the number of routes from point A to point B that begin by going up from point A (“up” relative to the orientation of the map) is the same as the number of routes from point A to point B that begin by going down from point A. Therefore, we only need to determine the number of routes from point A to point B that begin by going up and then double the result.
Tip If these two numbers of routes were not the same, or at least if it was not clear whether they were the same, then we would simply determine each of the numbers separately and then add them.
To determine the number of routes that begin by going up from point A, we can apply the Multiplication Principle. There are 3 locations at which branches occur. Moreover, at each of these locations, there are 3 different trails that can be taken. Finally, the choices of which trail to take at each location can be made independently. Therefore, the Multiplication Principle applies and we get (3)(3)(3) = 27 for the number of routes that begin by going up from point A. Hence, the number of routes from point A to point B is 2(27) = 54.
The correct answer is C.
It is clear that the number of routes from point A to point B that begin by going up from point A (“up” relative to the orientation of the map) is the same as the number of routes from point A to point B that begin by going down from point A. Therefore, we only need to determine the number of routes from point A to point B that begin by going up and then double the result.
Tip If these two numbers of routes were not the same, or at least if it was not clear whether they were the same, then we would simply determine each of the numbers separately and then add them.
To determine the number of routes that begin by going up from point A, we can apply the Multiplication Principle. There are 3 locations at which branches occur. Moreover, at each of these locations, there are 3 different trails that can be taken. Finally, the choices of which trail to take at each location can be made independently. Therefore, the Multiplication Principle applies and we get (3)(3)(3) = 27 for the number of routes that begin by going up from point A. Hence, the number of routes from point A to point B is 2(27) = 54.
The correct answer is C.
 加入收藏
加入收藏
 在线答疑
在线答疑
题目来源



























