题目信息
When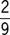 
of the votes on a certain resolution have been counted, 
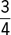of those counted are in favor of the resolution. What fraction of the remaining votes must be against the resolution so that the total count will result in a vote of 2 to 1 against the resolution?
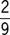of the votes on a certain resolution have been counted, 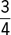of those counted are in favor of the resolution. What fraction of the remaining votes must be against the resolution so that the total count will result in a vote of 2 to 1 against the resolution?
A:
B:
C:
D:
E:
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
A:
Arithmetic Operations on rational numbers
For this problem, by assigning carefully chosen numbers to quantities given in the problem, it can be made more concrete and some of the computations with fractions can be avoided. Since
of all the votes have been counted and 
of them are for the resolution, 36 ( = 9 × 4) would be a good number to use as the total number of votes cast. Since the total count must result in a vote of 2 to 1 against the resolution, 
of all of the votes must be against the resolution. This information can be summarized in the following table.
From the table, it is clear that of the 28 votes still to be counted, 22 must be against the resolution. Therefore, the fraction of the votes still to be counted that must be against the resolution is
= 
.
In general, letting T represent the total number of votes cast, since the total count must result in a vote of 2 to 1 against the resolution,
T votes must be against the resolution. The information is summarized in the following table.
From the table, it is clear that of the
T votes still to be counted 
T must be against the resolution. Therefore, the fraction of the votes still to be counted that must be against the resolution is 
= 
.
The correct answer is A.
Alternative explanation:
Assign actual numbers to the problem to make the math more concrete. Since we are dealing with
of something and also 
of something, we will want our numbers to be convenient. Look for multiples of 36 (9 times 4) for which 
and will result in whole numbers. A number that will work well is 180.
Of the 180 votes, have been counted.
(180) = 40 votes counted. This means 140 votes have not been counted.
Of those 40 counted votes,
are in favor. 
(40) = 30 votes in favor (of the 40 counted).
This means 10 votes are not in favor (of the 40 counted).
Looking ahead to the desired end result, in order to achieve a 2:1 ratio against,
of the votes will be for and 
will be against. Therefore we will need 120 votes against. So far we have 10 votes not in favor.
In order to reach a total of 120 uncounted votes, of the 140 uncounted votes, we will need 110 votes not in favor to combine with the 10 counted votes not in favor.
This is
or 
. The correct answer is A.
For this problem, by assigning carefully chosen numbers to quantities given in the problem, it can be made more concrete and some of the computations with fractions can be avoided. Since
of all the votes have been counted and of them are for the resolution, 36 ( = 9 × 4) would be a good number to use as the total number of votes cast. Since the total count must result in a vote of 2 to 1 against the resolution, of all of the votes must be against the resolution. This information can be summarized in the following table.| Total votes cast | Counted so far | Still to be counted | |
| 36 |  (36) = 8 |
36 − 8 = 28 | |
| For |  (8) = 6 |
||
| Against |  (36) = 24 |
8 − 6 = 2 | 24 − 2 = 22 |
From the table, it is clear that of the 28 votes still to be counted, 22 must be against the resolution. Therefore, the fraction of the votes still to be counted that must be against the resolution is
= .In general, letting T represent the total number of votes cast, since the total count must result in a vote of 2 to 1 against the resolution,
T votes must be against the resolution. The information is summarized in the following table.| Total votes cast | Counted so far | Still to be counted | |
| T |  T |
T −  T =  T |
|
| For |   =  T |
||
| Against |  T |
  =  T |
 T −  T =  T |
From the table, it is clear that of the
T votes still to be counted T must be against the resolution. Therefore, the fraction of the votes still to be counted that must be against the resolution is = .The correct answer is A.
Alternative explanation:
Assign actual numbers to the problem to make the math more concrete. Since we are dealing with
of something and also of something, we will want our numbers to be convenient. Look for multiples of 36 (9 times 4) for which and will result in whole numbers. A number that will work well is 180.Of the 180 votes,
have been counted. (180) = 40 votes counted. This means 140 votes have not been counted.Of those 40 counted votes,
are in favor. (40) = 30 votes in favor (of the 40 counted).This means 10 votes are not in favor (of the 40 counted).
Looking ahead to the desired end result, in order to achieve a 2:1 ratio against,
of the votes will be for and will be against. Therefore we will need 120 votes against. So far we have 10 votes not in favor.In order to reach a total of 120 uncounted votes, of the 140 uncounted votes, we will need 110 votes not in favor to combine with the 10 counted votes not in favor.
This is
or . The correct answer is A.
加入收藏
在线答疑
题目来源
