题目信息
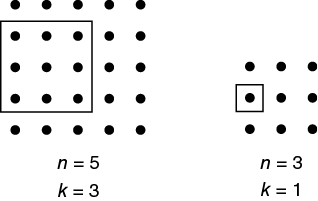
Let n and k be positive integers with k ≤ n. From an n × n array of dots, a k × k array of dots is selected. The figure above shows two examples where the selected k × k array is enclosed in a square. How many pairs (n, k) are possible so that exactly 48 of the dots in the n × n array are NOT in the selected k × k array?
A:1
B:2
C:3
D:4
E:5
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
C:3
Algebra Factoring; Simultaneous equations
The n × n array has n2 dots and the k × k array has k2 dots. The number of dots in the n × n array that are not in the k × k array is given by n2 – k2 = (n – k)(n + k).
Therefore, (n – k)(n + k) = 48 is a necessary condition for there to be 48 dots not in the k × k array. This is also a sufficient condition, since it is clear that at least one k × k array of dots can be selected for removal from an n × n array of dots when k ≤ n.
The equation (n – k)(n + k) = 48 represents two positive integers, namely n – k and n + k, whose product is 48. Thus, the smaller integer n – k must be 1, 2, 3, 4, or 6, and the larger integer n + k must be 48, 24, 16, 12, or 8. Rather than solving five pairs of simultaneous equations (for example, n – k = 2 and n + k = 24 is one such pair), it is more efficient to observe that the solution to the system n – k = a and n + k = b is
(add the equations, then divide by 2) and 
(substitute 
for n in either equation and solve for k; or subtract the equations, then divide by 2). Therefore, the possible pairs (n, k) arise exactly when 48 = ab and both a + b and b – a are divisible by 2. This occurs exactly three times—48 = (2)(24), 48 = (4)(12), and 48 = (6)(8).
The correct answer is C.
The n × n array has n2 dots and the k × k array has k2 dots. The number of dots in the n × n array that are not in the k × k array is given by n2 – k2 = (n – k)(n + k).
Therefore, (n – k)(n + k) = 48 is a necessary condition for there to be 48 dots not in the k × k array. This is also a sufficient condition, since it is clear that at least one k × k array of dots can be selected for removal from an n × n array of dots when k ≤ n.
The equation (n – k)(n + k) = 48 represents two positive integers, namely n – k and n + k, whose product is 48. Thus, the smaller integer n – k must be 1, 2, 3, 4, or 6, and the larger integer n + k must be 48, 24, 16, 12, or 8. Rather than solving five pairs of simultaneous equations (for example, n – k = 2 and n + k = 24 is one such pair), it is more efficient to observe that the solution to the system n – k = a and n + k = b is
(add the equations, then divide by 2) and (substitute for n in either equation and solve for k; or subtract the equations, then divide by 2). Therefore, the possible pairs (n, k) arise exactly when 48 = ab and both a + b and b – a are divisible by 2. This occurs exactly three times—48 = (2)(24), 48 = (4)(12), and 48 = (6)(8).The correct answer is C.
加入收藏
在线答疑
题目来源
