题目信息
If there is a least integer that satisfies the inequality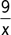 
≥ 2, what is that least integer?
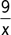≥ 2, what is that least integer?
A:0
B:1
C:4
D:5
E:There is not a least integer that satisfies the inequality.
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
B:1
Algebra Inequalities
It is clear that no negative integer satisfies the inequality (because
is false) and zero does not satisfy the inequality (because 
is undefined). Thus, the integers, if any, that satisfy 
≥ 2 must be among 1, 2, 3, 4, …. The least of these integers is 1, and it is easy to see that x = 1 satisfies the inequality 
≥ 2. Therefore, the least integer that satisfies the inequality is 1.
Alternatively, the inequality can be solved algebraically. It will be convenient to consider three cases according to whether x < 0, x = 0, and x > 0.
Case 1: Assume x < 0. Then multiplying both sides of the inequality by x, which is negative, gives 9 ≤ 2x, or x ≥ 4.5. Because we are assuming x < 0, there are no solutions to x ≥ 4.5. Therefore, no solutions exist in Case 1.
Case 2: Assume x = 0. Then
is not defined, and thus x = 0 cannot be a solution.
Case 3: Assume x > 0. Then multiplying both sides of the inequality by x, which is positive, gives 9 ≥ 2x, or x ≤ 4.5. Because we are assuming x > 0, the solutions that exist in Case 2 are all real numbers x such that 0 < x ≤ 4.5.
The set of all solutions to the inequality
≥ 2 will be all solutions found in Cases 1, 2, and 3. Therefore, the solutions to the inequality consist of all real numbers x such that 0 < x ≤ 4.5. The least of these solutions that is an integer is 1.
The correct answer is B.
It is clear that no negative integer satisfies the inequality (because
is false) and zero does not satisfy the inequality (because is undefined). Thus, the integers, if any, that satisfy ≥ 2 must be among 1, 2, 3, 4, …. The least of these integers is 1, and it is easy to see that x = 1 satisfies the inequality ≥ 2. Therefore, the least integer that satisfies the inequality is 1.Alternatively, the inequality can be solved algebraically. It will be convenient to consider three cases according to whether x < 0, x = 0, and x > 0.
Case 1: Assume x < 0. Then multiplying both sides of the inequality by x, which is negative, gives 9 ≤ 2x, or x ≥ 4.5. Because we are assuming x < 0, there are no solutions to x ≥ 4.5. Therefore, no solutions exist in Case 1.
Case 2: Assume x = 0. Then
is not defined, and thus x = 0 cannot be a solution.Case 3: Assume x > 0. Then multiplying both sides of the inequality by x, which is positive, gives 9 ≥ 2x, or x ≤ 4.5. Because we are assuming x > 0, the solutions that exist in Case 2 are all real numbers x such that 0 < x ≤ 4.5.
The set of all solutions to the inequality
≥ 2 will be all solutions found in Cases 1, 2, and 3. Therefore, the solutions to the inequality consist of all real numbers x such that 0 < x ≤ 4.5. The least of these solutions that is an integer is 1.The correct answer is B.
加入收藏
在线答疑
题目来源
