题目信息
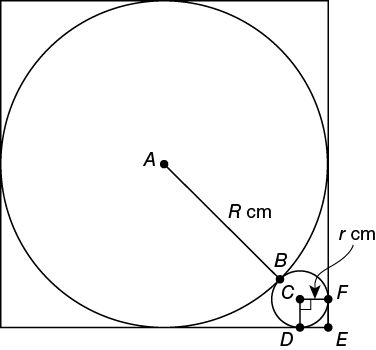
The figure above shows 2 circles. The larger circle has center A, radius R cm, and is inscribed in a square. The smaller circle has center C, radius r cm, and is tangent to the larger circle at point B and to the square at points D and F. If points A, B, C, and E are collinear, which of the following is equal to
?
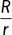A:
B:
C:
D:
E:
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
D:
Geometry Circles; Pythagorean theorem
Because
is a diagonal of square CDEF, which has side length r, it follows from the Pythagorean theorem that r2 + r2 = (CE)2, and hence CE = 
.
Tip A sometimes useful shortcut is the fact that, for a square we have d =
, where d is the diagonal length and s is the side length. This can be obtained by applying the Pythagorean theorem as above or by using properties of a 45–45–90 triangle.
Therefore, BE = r +
= r(1 + 
) and AE = R + r(1 + 
). Since 2(AE) is the diagonal length of the large square, which has side length 2R, it follows from the above tip that 2(AE) = (2R)
, or AE = R
. Alternatively, an appropriate application of the Pythagorean theorem gives R2 + R2 = (AE)2, or AE = R
. Now substitute for AE and solve for 
.
From the last equation we get
.
The correct answer is D.
Because
is a diagonal of square CDEF, which has side length r, it follows from the Pythagorean theorem that r2 + r2 = (CE)2, and hence CE = .Tip A sometimes useful shortcut is the fact that, for a square we have d =
, where d is the diagonal length and s is the side length. This can be obtained by applying the Pythagorean theorem as above or by using properties of a 45–45–90 triangle.Therefore, BE = r +
= r(1 + ) and AE = R + r(1 + ). Since 2(AE) is the diagonal length of the large square, which has side length 2R, it follows from the above tip that 2(AE) = (2R), or AE = R. Alternatively, an appropriate application of the Pythagorean theorem gives R2 + R2 = (AE)2, or AE = R. Now substitute for AE and solve for .From the last equation we get
.The correct answer is D.
加入收藏
在线答疑
题目来源
