题目信息
How many positive integers n have the property that both 3n and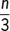 
are 4-digit integers?
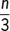are 4-digit integers?
A:111
B:112
C:333
D:334
E:1,134
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
B:112
Arithmetic Inequalities
If n is an integer, then 3n is always an integer. Also, 3n will be a 4-digit integer only when 1,000 ≤ 3n ≤ 9,999. Therefore, n is an integer such that 333
≤ n ≤ 3,333. Equivalently, n is an integer such that 334 ≤ n ≤ 3,333.
If n is an integer, then
is an integer only when n is a multiple of 3. Also, 
will be a 4-digit integer only when 1,000 ≤ 
≤ 9,999, or 3,000 ≤ n ≤ 29,997. Therefore, n is a multiple of 3 such that 3,000 ≤ n ≤ 29,997.
It follows that the values of n consist of all multiples of 3 between 3,000 = 3(1,000) and 3,333 = 3(1,111), inclusive. The number of such multiples of 3 is (1,111 − 1,000) + 1 = 112.
Tip Be alert to possible easily overlooked constraints that may exist in a problem. For example, in applying the second requirement above, it is not sufficient to only consider integer values of n such that 1,000 ≤
≤ 9,999. In addition, 
must also be an integer, and by applying this constraint it follows that the values of n must be multiples of 3.
The correct answer is B.
If n is an integer, then 3n is always an integer. Also, 3n will be a 4-digit integer only when 1,000 ≤ 3n ≤ 9,999. Therefore, n is an integer such that 333
≤ n ≤ 3,333. Equivalently, n is an integer such that 334 ≤ n ≤ 3,333.If n is an integer, then
is an integer only when n is a multiple of 3. Also, will be a 4-digit integer only when 1,000 ≤ ≤ 9,999, or 3,000 ≤ n ≤ 29,997. Therefore, n is a multiple of 3 such that 3,000 ≤ n ≤ 29,997.It follows that the values of n consist of all multiples of 3 between 3,000 = 3(1,000) and 3,333 = 3(1,111), inclusive. The number of such multiples of 3 is (1,111 − 1,000) + 1 = 112.
Tip Be alert to possible easily overlooked constraints that may exist in a problem. For example, in applying the second requirement above, it is not sufficient to only consider integer values of n such that 1,000 ≤
≤ 9,999. In addition, must also be an integer, and by applying this constraint it follows that the values of n must be multiples of 3.The correct answer is B.
加入收藏
在线答疑
题目来源
