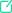题目信息
In the figure above, points A, B, C, and D are collinear and
, 
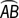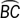, and 
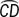are semicircles with diameters d1 cm, d2 cm, and d3 cm, respectively. What is the sum of the lengths of 
, 
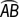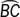, and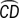 
, in centimeters?
A:Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B:Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C:BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D:EACH statement ALONE is sufficient.
E:Statements (1) and (2) TOGETHER are NOT sufficient.
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
B:Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Geometry Circles; Circumference
Since the circumference of a semicircle is
, it follows that 
has length 
cm, 
has length 
cm, and 
has length 
cm. Therefore, the sum of the lengths, in centimeters, of 
, , and 
is 
. Determine the value of 
.
Given that d1:d2:d3 is 3:2:1, it is not possible to determine the value of
because d1, d2, and d3 could be 3, 2, and 1 (d1 + d2 + d3 = 6) or d1, d2, and d3 could be 6, 4, and 2 (d1 + d2 + d3 = 12); NOT sufficient.
Given that AD = 48 and AD = d1 + d2 + d3, it follows that 
; SUFFICIENT.
The correct answer is B;statement 2 alone is sufficient.
Since the circumference of a semicircle is
, it follows that has length cm, has length cm, and has length cm. Therefore, the sum of the lengths, in centimeters, of , , and is . Determine the value of .Given that d1:d2:d3 is 3:2:1, it is not possible to determine the value of
because d1, d2, and d3 could be 3, 2, and 1 (d1 + d2 + d3 = 6) or d1, d2, and d3 could be 6, 4, and 2 (d1 + d2 + d3 = 12); NOT sufficient.
Given that AD = 48 and AD = d1 + d2 + d3, it follows that ; SUFFICIENT.The correct answer is B;statement 2 alone is sufficient.
加入收藏
在线答疑
题目来源
