题目信息
A large flower arrangement contains 3 types of flowers: carnations, lilies, and roses. Of all the flowers in the arrangement,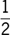 
are carnations, 
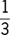are lilies, and 
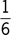are roses. The total price of which of the 3 types of flowers in the arrangement is the greatest?
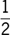are carnations, 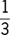are lilies, and 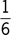are roses. The total price of which of the 3 types of flowers in the arrangement is the greatest?
A:Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B:Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C:BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D:EACH statement ALONE is sufficient.
E:Statements (1) and (2) TOGETHER are NOT sufficient.
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
A:Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Algebra Applied problems; Ratios
Let T be the total number of flowers, and let $C, $L, and $R be the cost, respectively, of one carnation, one lily, and one rose.
We are given that L = 3C (because C:L is 1:3) and R = 4C (because C:R is 1:4). The table below shows the total price for each type of flower.
From the table it is clear that lilies have the greatest total cost; SUFFICIENT.
We are given that R = 0.75 + C and R = 0.25 + L. To simplify matters, we can use these equations to express each of the variables C, L, and R in terms of a single fixed variable, for example, C = R −
and L = R − 
. This will allow us to replace all appearances of C, L, and R with appearances of R only, thereby reducing by two the number of variables that have to be dealt with. The table below shows, for two values of T and R, the total price for each type of flower.
From the table it is clear that the type of flower having the greatest total cost can vary; NOT sufficient.
Tip Consider the expressions under “Total price” in the previous table. Note that, for a fixed value of T, as the value of R increases without bound, the total price for carnation will eventually exceed the total price for each of the other two types of flowers. Therefore, for non-sufficiency of (2), it is only necessary to determine whether there exist values for T and R such that carnations do not have the greatest total price. This suggests trying a small value for R, for example R = 1. Also, note that T = 24 was chosen to avoid fractions in the computations—24 is divisible by both 8 and 12.
The correct answer is A;statement 1 alone is sufficient.
Let T be the total number of flowers, and let $C, $L, and $R be the cost, respectively, of one carnation, one lily, and one rose.
We are given that L = 3C (because C:L is 1:3) and R = 4C (because C:R is 1:4). The table below shows the total price for each type of flower.
| Flower | Number of flowers | Price per flower | Total price |
| Carnation |  |
C |  TC |
| Lily |  T |
3C | TC |
| Rose |  |
4C |  TC |
From the table it is clear that lilies have the greatest total cost; SUFFICIENT.
We are given that R = 0.75 + C and R = 0.25 + L. To simplify matters, we can use these equations to express each of the variables C, L, and R in terms of a single fixed variable, for example, C = R −
and L = R − . This will allow us to replace all appearances of C, L, and R with appearances of R only, thereby reducing by two the number of variables that have to be dealt with. The table below shows, for two values of T and R, the total price for each type of flower.| Flower | Number of flowers | Price per flower | Total price | Total price: T = 24, R = 1 | Total price: T = 24, R = 10 |
| Carnation |  T |
R −  |
 TR −  T |
3 | 111 |
| Lily |  T |
R −  |
 TR −  T |
6 | 78 |
| Rose |  T |
R |  TR |
4 | 40 |
From the table it is clear that the type of flower having the greatest total cost can vary; NOT sufficient.
Tip Consider the expressions under “Total price” in the previous table. Note that, for a fixed value of T, as the value of R increases without bound, the total price for carnation will eventually exceed the total price for each of the other two types of flowers. Therefore, for non-sufficiency of (2), it is only necessary to determine whether there exist values for T and R such that carnations do not have the greatest total price. This suggests trying a small value for R, for example R = 1. Also, note that T = 24 was chosen to avoid fractions in the computations—24 is divisible by both 8 and 12.
The correct answer is A;statement 1 alone is sufficient.
加入收藏
在线答疑
题目来源
