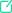题目信息
A bank account earned 2% annual interest, compounded daily, for as long as the balance was under $1,000, starting when the account was opened. Once the balance reached $1,000, the account earned 2.5% annual interest, compounded daily until the account was closed. No deposits or withdrawals were made. Was the total amount of interest earned at the 2% rate greater than the total amount earned at the 2.5% rate?
A:Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B:Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C:BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D:EACH statement ALONE is sufficient.
E:Statements (1) and (2) TOGETHER are NOT sufficient.
参考答案及共享解析
共享解析来源为网络权威资源、GMAT高分考生等； 如有疑问，欢迎在评论区提问与讨论
本题耗时：
已选答案：
正确答案：
C:BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
Algebra Applied problems
Let P0, P1, and P2 be the initial balance, the balance after one year, and the balance after two years.
Since $25 is the exact amount of interest earned in one year by an initial amount of $1,000 earning 2.5 percent annual interest, compounded yearly, it follows that $25 is the total amount of interest earned in slightly less than one year by an initial amount of $1,000 earning 2.5 percent annual interest, compounded daily. However, the total amount of interest earned at the 2 percent rate could be less than $25 (for example, if P0 = $990, then the interest earned at the 2 percent rate is $10) and the total amount of interest earned at the 2 percent rate could be greater than $25 (for example, if P0 = $900, then the interest earned at the 2 percent rate is $100); NOT sufficient. Given that the account was open for exactly three years, then the total amount of interest at the 2 percent rate could be less than the total amount of interest at the 2.5 percent rate (for example, if the balance reached $1,000 a few days after the account was open). On the other hand, the total amount of interest at the 2 percent rate could also be greater than the total amount of interest at the 2.5 percent rate (for example, if the balance reached $1,000 a few days before the account was closed); NOT sufficient.
Given (1) and (2), it follows that the account earned interest at the 2.5 percent rate for slightly less than one year and the account earned interest at the 2 percent rate for slightly more than two years. Therefore, the balances of P1 and P2 were reached while the account was earning interest at the 2 percent rate. Since P0(1.02) < P1 and P1(1.02) < P2 (compounding daily for one year produces a greater amount than compounding annually for one year), the values of P0, P1, and P2 satisfy the following inequalities.
P0 < P0(1.02) < P1 < P1(1.02) < P2 < 1,000
Note that the difference 1,000 – P0 is the total amount of interest earned at the 2 percent rate. Thus, using (2), we wish to determine whether this difference is greater than 25. From P0(1.02) < P1 it follows that P0(1.02)2 < P1(1.02), and since P1(1.02) < 1,000, we have P0(1.02)2 < 1,000. Therefore, P0 <
, from which we can conclude the following inequality.
Since 1,000 −
> 25 (see below), it follows that 1,000 − P0 > 25 and hence the total amount of interest earned at the 2 percent rate is greater than the total amount of interest earned at the 2.5 percent rate.
One way to verify that 1,000 –
> 25 is to verify that 1 – 
, or equivalently, verify that 
, or 40 < 39(1.02)2. Now note that we can obtain this last inequality from 40 < 39(1.04) (because 39 + 39(0.04) is greater than 39 + 1) and 1.04 < (1.02)2.
The correct answer is C; both statements together are sufficient.
Let P0, P1, and P2 be the initial balance, the balance after one year, and the balance after two years.
Since $25 is the exact amount of interest earned in one year by an initial amount of $1,000 earning 2.5 percent annual interest, compounded yearly, it follows that $25 is the total amount of interest earned in slightly less than one year by an initial amount of $1,000 earning 2.5 percent annual interest, compounded daily. However, the total amount of interest earned at the 2 percent rate could be less than $25 (for example, if P0 = $990, then the interest earned at the 2 percent rate is $10) and the total amount of interest earned at the 2 percent rate could be greater than $25 (for example, if P0 = $900, then the interest earned at the 2 percent rate is $100); NOT sufficient. Given that the account was open for exactly three years, then the total amount of interest at the 2 percent rate could be less than the total amount of interest at the 2.5 percent rate (for example, if the balance reached $1,000 a few days after the account was open). On the other hand, the total amount of interest at the 2 percent rate could also be greater than the total amount of interest at the 2.5 percent rate (for example, if the balance reached $1,000 a few days before the account was closed); NOT sufficient.
Given (1) and (2), it follows that the account earned interest at the 2.5 percent rate for slightly less than one year and the account earned interest at the 2 percent rate for slightly more than two years. Therefore, the balances of P1 and P2 were reached while the account was earning interest at the 2 percent rate. Since P0(1.02) < P1 and P1(1.02) < P2 (compounding daily for one year produces a greater amount than compounding annually for one year), the values of P0, P1, and P2 satisfy the following inequalities.
P0 < P0(1.02) < P1 < P1(1.02) < P2 < 1,000
Note that the difference 1,000 – P0 is the total amount of interest earned at the 2 percent rate. Thus, using (2), we wish to determine whether this difference is greater than 25. From P0(1.02) < P1 it follows that P0(1.02)2 < P1(1.02), and since P1(1.02) < 1,000, we have P0(1.02)2 < 1,000. Therefore, P0 <
, from which we can conclude the following inequality.Since 1,000 −
> 25 (see below), it follows that 1,000 − P0 > 25 and hence the total amount of interest earned at the 2 percent rate is greater than the total amount of interest earned at the 2.5 percent rate.One way to verify that 1,000 –
> 25 is to verify that 1 – , or equivalently, verify that , or 40 < 39(1.02)2. Now note that we can obtain this last inequality from 40 < 39(1.04) (because 39 + 39(0.04) is greater than 39 + 1) and 1.04 < (1.02)2.The correct answer is C; both statements together are sufficient.
加入收藏
在线答疑
题目来源
